Summary

In statistics, an outlier is defined as an observation which stands far away from the most of other observations. An outlier can be a result of a measurement error and the inclusion of that error would have a great impact on the analysis results. Therefore, every data set should be scanned for possible outliers before conducting any statistical analysis. Like missing values, detecting outliers and dealing with them are also crucial in the data preprocessing. In this module, first you will learn how to identify univariate and multivariate outliers using descriptive, graphical and distance-based methods. Then, you will learn different approaches to deal with these values using R.

Learning Objectives

The learning objectives of this module are as follows:

• Identify the outlier(s) in the data set.
• Apply descriptive methods to identify univariate outliers.
• Apply graphical approaches to scan for univariate or multivariate outliers.
• Apply distance-based metrics to identify univariate or multivariate outliers.
• Learn commonly used approaches to handle outliers.

Types of Outliers

Outlier can be univariate and multivariate. Univariate outliers can be found when looking at a distribution of values in a single variable. The example given above is an example of a univariate outlier as we only look at the distribution of income (i.e., one variable) among our customers. On the other hand, multivariate outliers can be found in a n-dimensional space (of n-variables). In order to find them, we need to look at distributions in multi-dimensions.

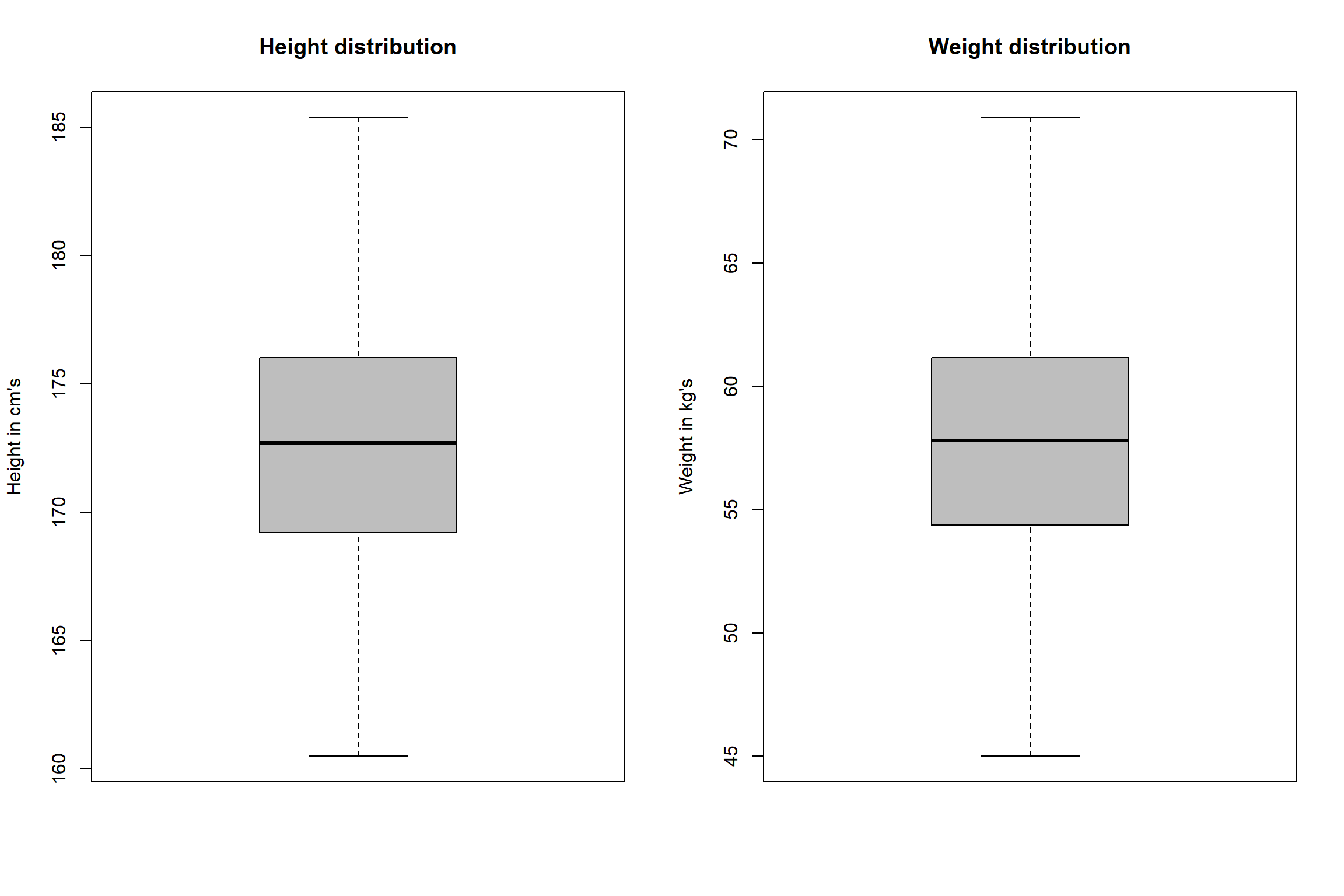
To illustrate multivariate outliers, let’s assume that we are interested in understanding the relationship between height and weight. Below, we have univariate and bivariate distribution for Height and Weight. When we look at the univariate distributions of Height and Weight (i.e., using boxplots) separately, we don’t spot any abnormal cases (i.e. above and below the 1.5×IQR fence). However, when we look at the bivariate (two dimensional) distribution of Height and Weight (using scatter plot), we can see that we have one observation whose weight is 45.19 kg and height is 185.09 (on the upper-left side of the scatter plot). This observation is far away from most of the other weight and height combinations thus, will be seen as a multivariate outlier.

Most Common Causes of Outliers

Often an outlier can be a result of data entry errors, measurement errors, experimental errors, intentional errors, data processing errors or due to the sampling (i.e., sampling error). The following are the most common causes of outliers (taken from: https://www.analyticsvidhya.com/blog/2016/01/guide-data-exploration/)

• Data Entry Error: Outliers can arise because of the human errors during data collection, recording, or entry.

• Measurement Error: It is the most common source of outliers. This is caused when the measurement instrument used turns out to be faulty.

• Experimental Error: Another cause of outliers is the experimental error. Experimental errors can arise during data extraction, experiment/survey planning and executing errors.

• Intentional Error: This type of outlier is commonly found in self-reported measures that involves sensitive data. For example, teens would typically under report the amount of alcohol that they consume. Only a fraction of them would report actual value. Here actual values might look like outliers because rest of the teens are under reporting the consumption.

• Data Processing Error: Often, due to the data sets are extracted from multiple sources, it is possible that some manipulation or extraction errors may lead to outliers in the data set.

• Sampling Error: Sometimes, outliers can arise due to the sampling (taking samples from population) process. Typically, this type of outliers can be seen when we take a few observations as a sample.

Univariate Outlier Detection Methods

One of the simplest methods for detecting univariate outliers is the use of boxplots. A boxplot is a graphical display for describing the distribution of the data using the median, the first (Q1) and third quartiles (Q3), and the inter-quartile range (IQR=Q3−Q1). Below is an illustration of a typical boxplot (taken from [Dr. James Baglin’s Intro to Stats website] (https://astral-theory-157510.appspot.com/secured/MATH1324_Module_02.html#box_plots)).

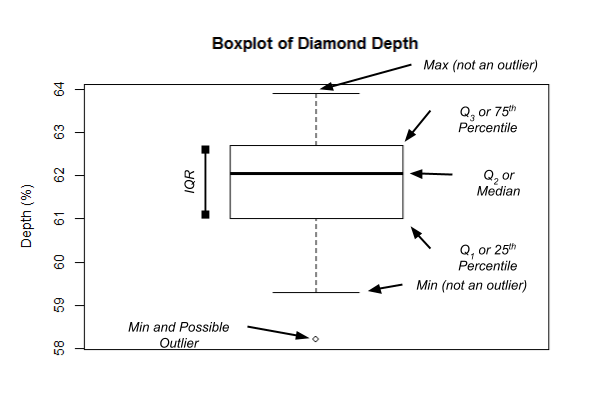
In the boxplot, the “Tukey’s method of outlier detection” is used to detect outliers. According to this method, outliers are defined as the values in the data set that fall beyond the range of −1.5×IQR to 1.5×IQR. These −1.5×IQR and 1.5×IQR limits are called “outlier fences” and any values lying outside the outlier fences are depicted using an “o” or a similar symbol on the boxplot.

Note that Tukey’s method is a nonparametric way of detecting outliers, therefore it is mainly used to test outliers in non-symmetric/ non-normal data distributions.

In order to illustrate the boxplot, we will use the Diamonds.csv data set available under the data repository.

Diamonds <- read.csv("data/Diamonds.csv")
head(Diamonds)

##   carat       cut color clarity depth table price    x    y    z
## 1  0.23     Ideal     E     SI2  61.5    55   326 3.95 3.98 2.43
## 2  0.21   Premium     E     SI1  59.8    61   326 3.89 3.84 2.31
## 3  0.23      Good     E     VS1  56.9    65   327 4.05 4.07 2.31
## 4  0.29   Premium     I     VS2  62.4    58   334 4.20 4.23 2.63
## 5  0.31      Good     J     SI2  63.3    58   335 4.34 4.35 2.75
## 6  0.24 Very Good     J    VVS2  62.8    57   336 3.94 3.96 2.48

We can use boxplot() function (under Base graphics) to get the boxplot of the carat variable:

Diamonds$carat %>%  boxplot(main="Boxplot of Diamond Carat", ylab="Carat", col = "grey")

According to the Tukey’s method, the carat variable seems to have many outliers. In the next section, we will discuss different approaches to handle these outliers.

There are also distance based methods to detect univariate outliers. One of them is to use the z- scores (i.e., normal scores) method. In this method, a standardised score (z-score) of all observations are calculated using the following equation:

zi=Xi−ˉXS

In the equation below, Xi denotes the values of observations, ˉX and S are the sample mean and standard deviation, respectively. An observation is regarded as an outlier based on its z-score, if the absolute value of its z-score is greater than 3.

Note that, z-score method is a parametric way of detecting outliers and assumes that the underlying data is normally distributed. Therefore, if the distribution is not approximately normal, this method shouldn’t be used. 

In order to illustrate the z- score approach, we will use the “outliers package”. The outliers package provides several useful functions to systematically extract outliers. Among those, the scores() function will calculate the z-scores (in addition to the t, chi-square, IQR, and Median absolute deviation scores) for the given data. Note that, there are many alternative functions in R for calculating z-scores. You may also use these functions and detect the outliers.

Let’s investigate any outliers in the depth variable using z-score approach. First, we will make sure that the depth distribution is approximately normal. For this purpose we can use histogram (or boxplot()) to check the distribution:

hist(Diamonds$depth)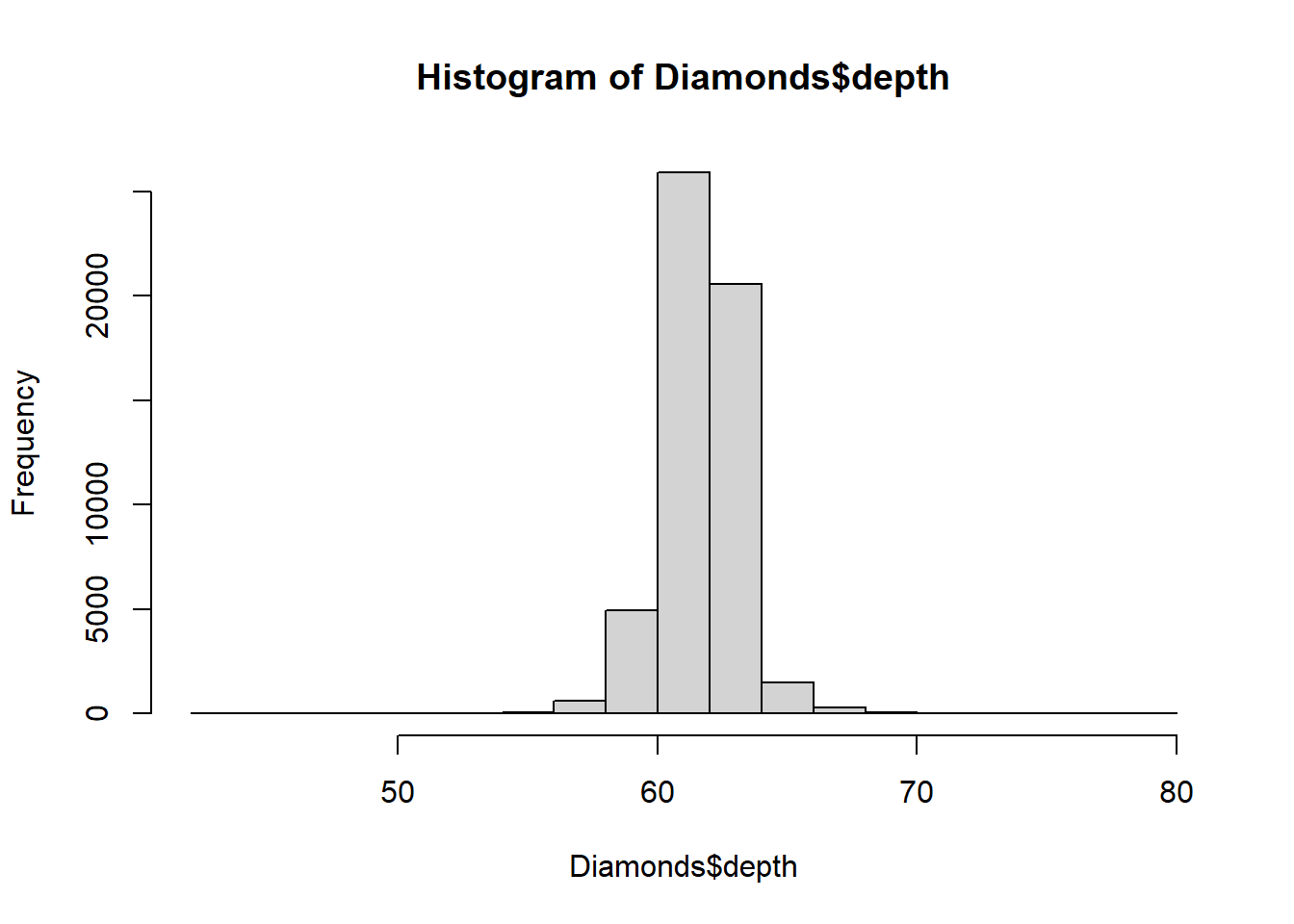

After confirming the depth variable has an approximately normal distribution, we can calculate z scores using outliers package:

library(outliers)
z.scores <- Diamonds$depth %>%  scores(type = "z")
z.scores %>% summary()

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -13.08748  -0.52310   0.03532   0.00000   0.52393  12.04128

From the summary() output, we can see that the minimum z score is -13.08 and the maximum is 12.04. 

Using which(), we can also find the locations of the z-scores whose absolute value is greater than 3.

# Finds the locations of outliers in the depth variable

which(abs(z.scores) >3 )

##   [1]     3    92    98   205   222   228   299   353   370   386   424   441
##  [13]   444   529   636   713   714   715   720   751   772   778   802   840
##  [25]   896   899   900   920   930   939   940  1099  1228  1239  1268  1439
##  [37]  1600  1609  1676  1683  1796  1811  1812  1883  1907  2016  2025  2026
##  [49]  2086  2113  2132  2178  2183  2184  2213  2217  2230  2314  2337  2353
##  [61]  2357  2367  2412  2447  2480  2498  2505  2582  2584  2699  2746  2874
##  [73]  2890  2914  2935  2982  2991  3152  3185  3421  3447  3565  3597  3754
##  [85]  3837  4024  4145  4152  4208  4274  4308  4326  4327  4328  4416  4506
##  [97]  4513  4519  4602  4655  4669  4696  4780  4789  4808  4886  4925  4971
## [109]  4972  5005  5007  5015  5034  5140  5354  5447  5461  5463  5470  5499
## [121]  5558  5576  5591  5699  5707  5740  5744  5776  5846  5870  5922  5935
## [133]  6021  6061  6163  6166  6341  6342  6348  6402  6430  6466  6493  6503
## [145]  6564  6628  6631  6656  6678  6741  6752  6796  6813  6816  6920  6940
## [157]  6971  6994  7023  7024  7097  7102  7172  7375  7417  7594  7675  7700
## [169]  7705  7738  7774  7821  7901  8010  8015  8160  8187  8188  8203  8357
## [181]  8393  8412  8456  8509  8576  8620  8673  8722  8854  8856  8866  8890
## [193]  8894  9098  9121  9282  9465  9604  9677  9735  9785  9874  9908  9950
## [205]  9981  9982  9983 10172 10271 10291 10378 10465 10474 10498 10594 10657
## [217] 10658 10690 10761 10814 10937 10962 11091 11114 11130 11161 11242 11313
## [229] 11370 11628 11758 11779 11828 11911 12132 12187 12233 12270 12281 12424
## [241] 12477 12619 12646 12815 12830 13003 13126 13222 13248 13270 13271 13279
## [253] 13563 13724 13758 13923 13992 13993 14039 14114 14129 14139 14456 14505
## [265] 14646 14668 14848 14882 14914 15000 15062 15147 15228 15314 15350 15504
## [277] 15624 15644 15670 15685 15782 15812 15816 15850 15866 15941 16085 16123
## [289] 16257 16328 16409 16440 16502 16505 16534 16638 16858 17025 17098 17182
## [301] 17197 17223 17314 17476 17482 17490 17553 17594 17692 17718 17720 17957
## [313] 18025 18073 18358 18359 18462 18531 18545 18686 18816 19016 19153 19184
## [325] 19247 19289 19332 19347 19407 19503 19590 19786 19793 19985 20103 20338
## [337] 20442 20648 20878 21157 21449 21513 21574 21602 21603 21685 21712 21713
## [349] 21737 22005 22030 22052 22461 22573 22594 22621 22668 22732 22742 22756
## [361] 22832 22872 23021 23176 23196 23287 23289 23490 23568 23645 24036 24242
## [373] 24245 24349 24524 24599 24892 24992 25025 25138 25281 25341 25351 25389
## [385] 25441 25452 25566 25730 25900 26067 26100 26249 26264 26265 26389 26432
## [397] 26491 26560 26651 27165 27352 27624 27634 27647 28271 30045 30375 30719
## [409] 30720 31231 31245 31251 31616 32073 32470 32507 32902 33016 33017 33103
## [421] 33524 33920 34252 34582 34699 35073 35119 35233 35663 35915 36044 36504
## [433] 36571 36673 36818 36819 36822 36835 36933 36959 37112 37217 37220 37276
## [445] 37304 37330 37506 37677 37678 37699 37701 37746 37781 37814 38041 38042
## [457] 38054 38154 38174 38315 38443 38550 38642 38841 39061 39088 39220 39254
## [469] 39308 39319 39386 39566 39679 39739 39842 39907 39914 40019 40026 40330
## [481] 40419 40421 40422 40434 40474 40485 40531 40615 40674 40695 40709 40767
## [493] 40772 40875 40900 40970 41061 41126 41331 41504 41506 41547 41660 41695
## [505] 41776 41821 41842 41857 41878 41919 42013 42092 42105 42120 42142 42192
## [517] 42257 42394 42447 42513 42548 42575 42644 42718 42805 42903 42905 42987
## [529] 42988 43177 43217 43386 43399 43481 43584 43706 43716 43777 43847 44040
## [541] 44155 44158 44212 44501 44533 44867 45035 45058 45067 45251 45535 45615
## [553] 45689 45760 45829 46093 46203 46346 46348 46361 46379 46431 46450 46477
## [565] 46558 46574 46611 46666 46680 46716 46785 46791 46824 46843 46891 46911
## [577] 47110 47126 47304 47604 47741 47776 47783 47912 47920 48093 48132 48242
## [589] 48260 48489 48499 48558 48607 48627 48706 48745 48855 48885 49100 49208
## [601] 49250 49265 49496 49508 49539 49653 49719 49774 49806 49883 49940 50004
## [613] 50039 50328 50380 50522 50583 50603 50747 50774 50907 51008 51049 51086
## [625] 51118 51123 51125 51140 51151 51203 51259 51392 51425 51463 51465 51497
## [637] 51514 51572 51622 51629 51692 51709 51718 51732 51840 51869 51929 51971
## [649] 52040 52084 52112 52245 52269 52345 52394 52460 52471 52475 52539 52566
## [661] 52569 52590 52594 52676 52677 52704 52707 52806 52849 52861 52862 52994
## [673] 53065 53123 53155 53435 53496 53541 53543 53661 53728 53757 53758 53801
## [685] 53864

# Finds the total number of outliers according to the z-score

length (which(abs(z.scores) >3 ))

## [1] 685

According to the z-score method, the depth variable has 685 outliers.

There are also many statistical tests to detect outliers. Some of them are the Chi-square test for outliers, the Cochran’s test, the Dixon test and the Grubbs test. In this course, we won’t cover these statistical testing approaches used for detecting outliers. You may refer to the [outliers package manual] (https://cran.r-project.org/web/packages/outliers/outliers.pdf) which includes useful functions for the commonly used outlier tests as well as the distance-based approaches.

Multivariate Outlier Detection Methods

When we have only two variables, the bivariate visualisation techniques like bivariate boxplots and scatter plots, can easily be used to detect any outliers.

To illustrate the bivariate, we will assume that we are only interested in one numerical carat variable and a one factor (quantitative) cut variable in the Diamonds data set.

boxplot(Diamonds$carat ~ Diamonds$cut, main="Diamond carat by cut", ylab = "Carat", xlab = "Cut")

Using the univariate boxplot approach, we can easily detect outliers in carat for a given cut.

Another bivariate visualisation method is the scatter plots. These plots are used to visualise the relationship between two quantitative variables. They are also very useful tools to detect obvious outliers for the two-dimensional data (i.e., for two continuous variables).

The plot() function will be used to get the scatter plot and detect outliers in carat and depth variables:

Diamonds %>% plot(carat ~ depth, data = ., ylab="Carat", xlab="Depth", main="Carat by Depth")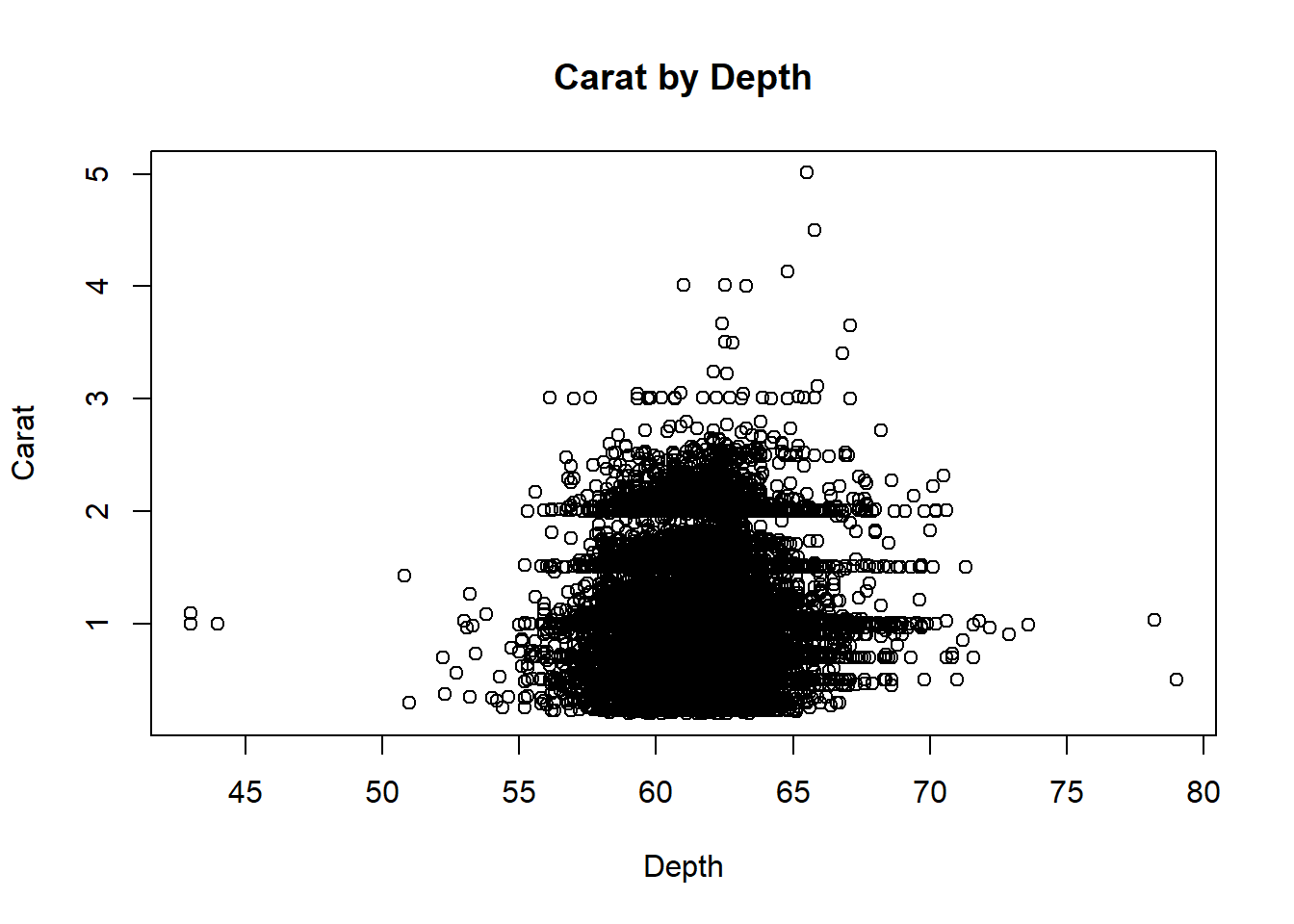

According to the scatter plot, there are some possible outliers on the lower left (the data points where both carat and depth is small) and lower right-hand side of the scatter (the data points with larger depth but small carat values).

Scatter plots are useful methods to detect abnormal observations for a given pair of variables. However, when there are more than two variables, scatter plots can no longer be used. For such cases, multivariate distance-based methods of outlier detection can be used.

The Mahalanobis distance is the most commonly used distance metric to detect outliers for the multivariate setting. The Mahalanobis distance is simply an extension of the univariate z-score, which also accounts for the correlation structure between all the variables. Mahalanobis distance follows a Chi-square distribution with n (number of variables) degrees of freedom, therefore any Mahalanobis distance greater than the critical chi-square value is treated as outliers.

I will not go into details of calculation of the Mahalanobis distance. We will use the MVN package to get these distances as it will also provide us the useful Mahalanobis distance vs. Chi-square quantile distribution plot (QQ plot) and contour plots. For more information on this package and its capabilities please refer to the paper on https://cran.r-project.org/web/packages/MVN/MVN.pdf.

To illustrate the usage of this package to detect multivariate outliers, we will use a subset of the Iris data, which is versicolor flowers, with the first three variables (Sepal.Length, Sepal.Width and Petal.Length).

First let’s read the data using:

# load iris data and subset using versicolor flowers, with the first three variables

iris <- read.csv("data/iris.csv")
versicolor <- iris %>%  filter(Species == "versicolor" ) %>%  dplyr::select(Sepal.Length, Sepal.Width, Petal.Length)
head(versicolor)

##   Sepal.Length Sepal.Width Petal.Length
## 1          7.0         3.2          4.7
## 2          6.4         3.2          4.5
## 3          6.9         3.1          4.9
## 4          5.5         2.3          4.0
## 5          6.5         2.8          4.6
## 6          5.7         2.8          4.5

The mvn() function under MVN package (Korkmaz, Goksuluk, and Zararsiz (2014)) lets us to define the multivariate outlier detection method using the multivariateOutlierMethod argument. When we use multivariateOutlierMethod = "quan" argument, it detects the multivariate outliers using the chi-square distribution critical value approach mentioned above. The showOutliers = TRUE argument will depict any multivariate outliers and show them on the QQ plot.

# Multivariate outlier detection using Mahalanobis distance with QQ plots
 
results <- mvn(data = versicolor, multivariateOutlierMethod = "quan", showOutliers = TRUE)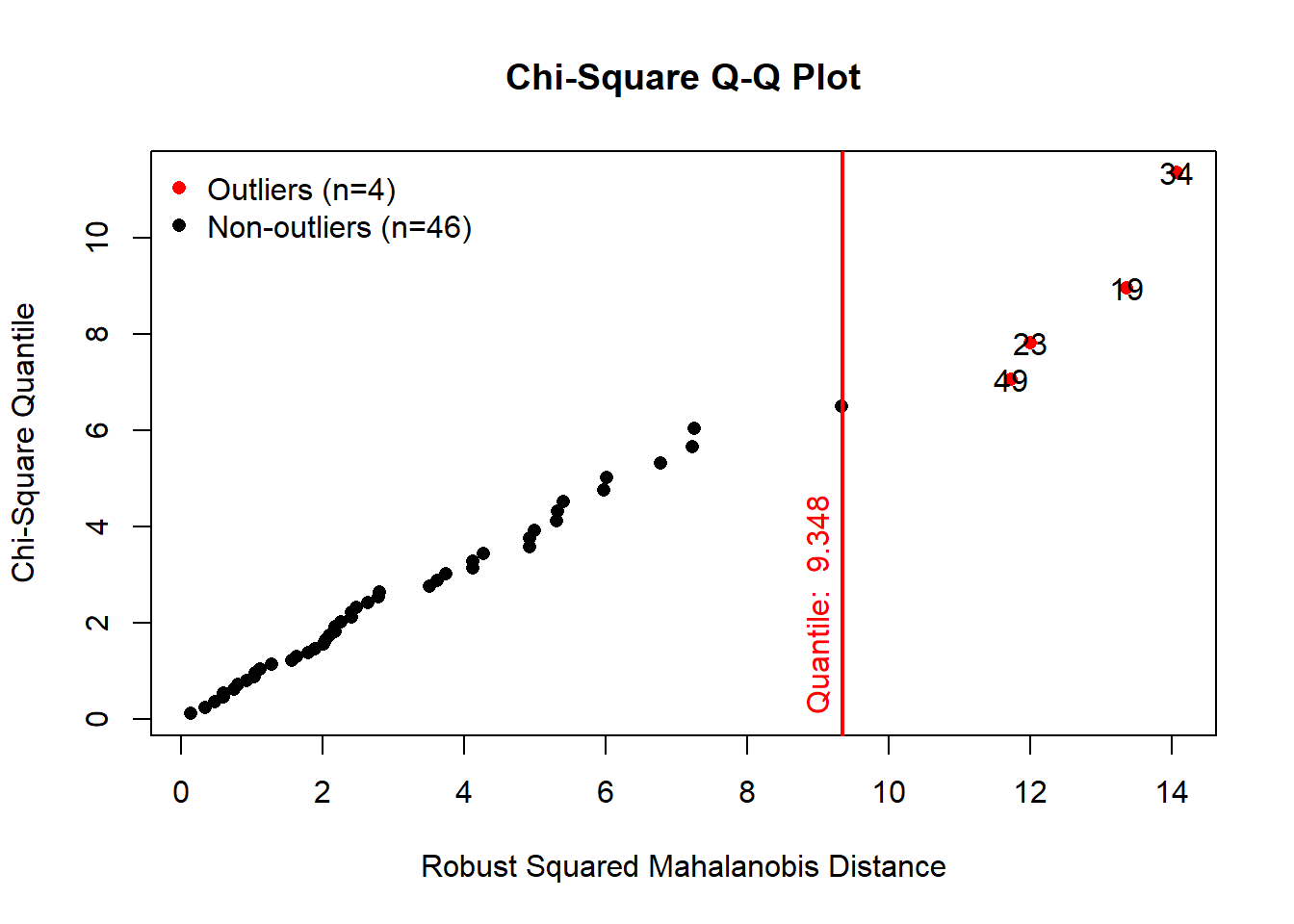

As we can see on the QQ plot, the Mahalonobis distance suggests existence of four outliers for this subset of the iris data.

If we would like to see the list of possible multivariate outliers, we can use result$multivariateOutliers to select only the results related to outliers as follows:

results$multivariateOutliers

##    Observation Mahalanobis Distance Outlier
## 34          34               14.065    TRUE
## 19          19               13.360    TRUE
## 23          23               12.005    TRUE
## 49          49               11.729    TRUE

This output is very useful in terms of providing the locations of outliers in the data set. In our example the 34st, 19th, 23rd and 49th observations are the suggested outliers for this subset of iris data.

The mvn() function has also different plot options to help discovering possible multivariate outliers. For example, to get the bivariate contour plots, we can use multivariatePlot = "contour" argument. However, note that contour plots can only be used for two variables.

Let’s illustrate the contour plots on the subset of setosa flowers, with the first two variables, Sepal.Length and Sepal.Width.

# load iris data and subset using setosa flowers, with the first two variables

setosa <- iris %>%  filter( Species == "setosa" ) %>%  dplyr::select(Sepal.Length, Sepal.Width)
head(setosa)

##   Sepal.Length Sepal.Width
## 1          5.1         3.5
## 2          4.9         3.0
## 3          4.7         3.2
## 4          4.6         3.1
## 5          5.0         3.6
## 6          5.4         3.9

# Multivariate outlier detection using Mahalanobis distance with contour plots

results <- mvn(data = setosa, multivariateOutlierMethod = "quan", multivariatePlot = "contour")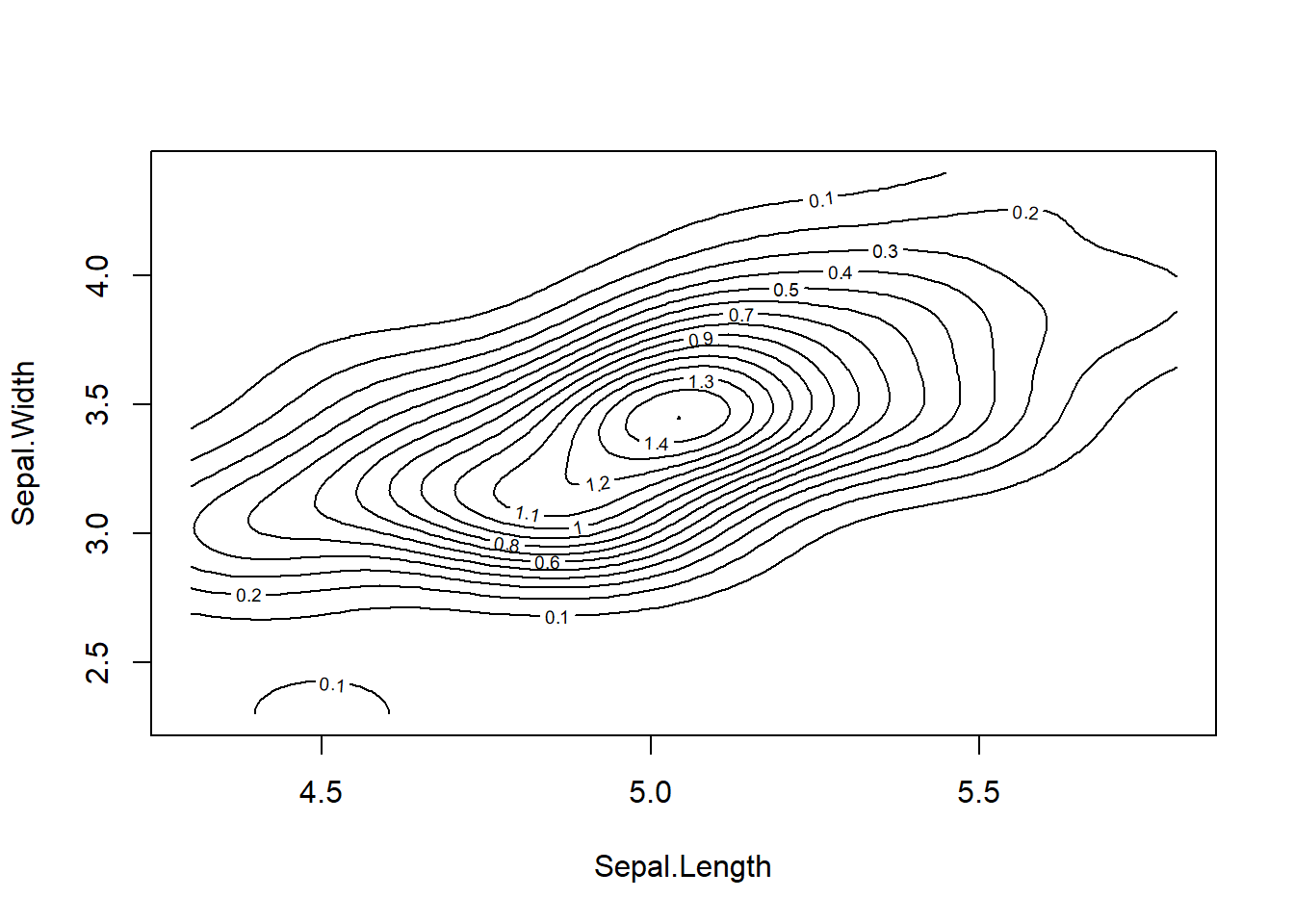

From the contour plot, we can see one anomality on the left-hand side of the plot, however, according to the QQ plot, this abnormal case doesn’t seem to be an outlier as its Mahanolobis distance didn’t exceed the threshold chi-square value.

The Minimum Covariance Determinant (MCD) is another approach for multivariate outliers. The cov.mcd function under MASS package lets us to define the multivariate outlier detection method. For more information on this function please refer to the paper Detecting multivariate outliers written by Leys, C. et.al. (2018) and the samples from Handling Multivariate Outliers.

Some applications of univariate and multivariate outlier detection can extend from fraud detection (i.e., unusual purchasing behaviour of a credit card owner), medicine (i.e. detection of unusual symptoms of a patient), sports statistics (i.e., abnormal performance for players may indicate doping), measurement errors (i.e., abnormal values could provide an indication of a measurement error), etc. Like missing value analysis, univariate and multivariate outlier analyses are also broader concepts. There are also different distance-based and probabilistic methods (like clustering analysis, genetic algorithm, etc.) that can be used to detect outliers in the high dimensional data sets. There is a huge theory behind the outlier detection methods and outlier analysis would be a standalone topic of another course. Interested readers may refer to the “Outlier analysis, by Charu C. Aggarwal” for the theory behind the outlier detection methods (Aggarwal (2015)).

Excluding or Deleting Outliers

Some authors recommend that if the outlier is due to data entry error, data processing error or outlier observations are very small in numbers, then leaving out or deleting the outliers would be used as a strategy. When this is the case, we can exclude/delete outliers in a couple different ways.

To illustrate, let’s revisit the outliers in the carat variable. Remember that we already found the locations of the outliers in the carat variable using which() function. Intuitively, we can exclude these observations from the data using:

Carat_clean<- Diamonds$carat[ - which( abs(z.scores) >3 )]

Let’s see another example on the previous versicolor data:

versicolor <- iris %>%  filter(Species == "versicolor" ) %>%  dplyr::select(Sepal.Length, Sepal.Width,Petal.Length)
head(versicolor)

##   Sepal.Length Sepal.Width Petal.Length
## 1          7.0         3.2          4.7
## 2          6.4         3.2          4.5
## 3          6.9         3.1          4.9
## 4          5.5         2.3          4.0
## 5          6.5         2.8          4.6
## 6          5.7         2.8          4.5

results <- mvn(data = versicolor, multivariateOutlierMethod = "quan", showOutliers = TRUE)

results$multivariateOutliers

##    Observation Mahalanobis Distance Outlier
## 34          34               14.065    TRUE
## 19          19               13.360    TRUE
## 23          23               12.005    TRUE
## 49          49               11.729    TRUE

The Mahalonobis distance method provided us the locations of outliers in the data set. In our example the 34st, 19th, 23rd and 49th observations are the suggested outliers. Using the basic filtering and subsetting functions, we can easily exclude these two outliers:

# Exclude 34st, 19th, 23rd and 49th observations

versicolor_clean <- versicolor[ -c(19,23,34,49), ]

# Check the dimension and see outliers are excluded

dim(versicolor_clean)

## [1] 46  3

Note that, the mvn() function also has an argument called showNewData = TRUE to exclude the outliers. One can simply detect and remove outliers using the following argument:

versicolor_clean2 <- mvn(data = versicolor, multivariateOutlierMethod = "quan", showOutliers = TRUE, showNewData = TRUE)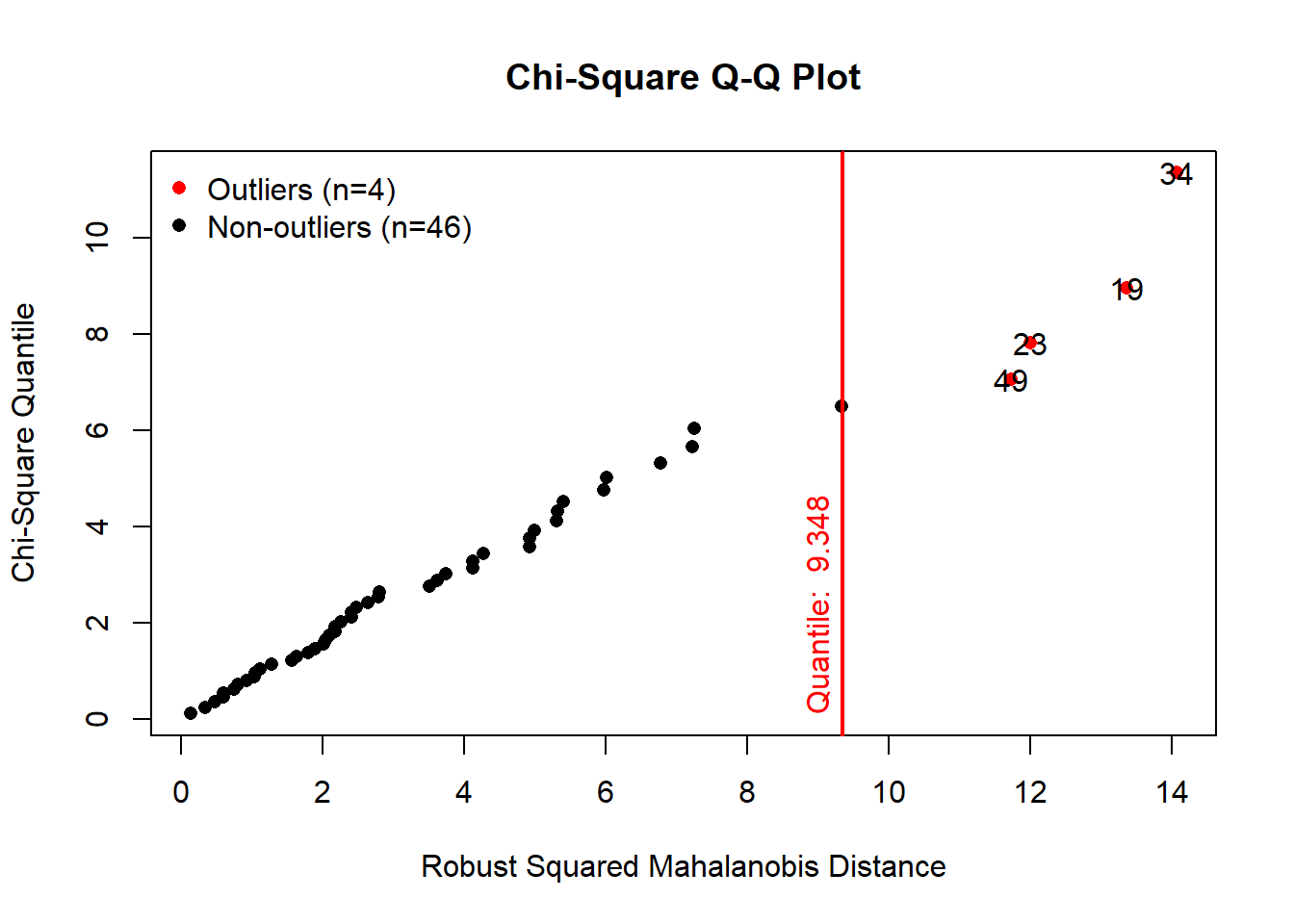

# Prints the data without outliers

dim(versicolor_clean2$newData)

## [1] 46  3

Imputing

Like imputation of missing values, we can also impute outliers. We can use mean (need to be used with caution!), median imputation or capping methods to replace outliers. Before imputing values, we should analyse the distribution carefully, and investigate whether the suggested outlier is a result of data entry/processing error. If the outlier is due to a data entry/processing error, we can go with imputing values.

For the illustration purposes, let’s replace the two outlier values in carat variable with its mean by using Base R functions:

Diamonds <- read.csv("data/Diamonds.csv")
Diamonds$carat[ which( abs(z.scores) >3 )] <- mean(Diamonds$carat, na.rm = TRUE)

Replacing outliers with the median or a user specified value can also be done using a similar approach. Note that, you may also prefer to write your own functions to deal with outliers.

Capping (a.k.a Winsorising)

Capping or winsorising involves replacing the outliers with the nearest neighbours that are not outliers. For example, for outliers that lie outside the outlier fences on a boxplot, we can cap it by replacing those observations outside the lower limit with the value of 5th percentile and those that lie above the upper limit, with the value of 95th percentile.

In order to cap the outliers we can use a user-defined function as follows (taken from: Stackoverflow):

# Define a function to cap the values outside the limits

cap <- function(x){
    quantiles <- quantile( x, c(.05, 0.25, 0.75, .95 ) )
    x[ x < quantiles[2] - 1.5*IQR(x) ] <- quantiles[1]
    x[ x > quantiles[3] + 1.5*IQR(x) ] <- quantiles[4]
    x}

To illustrate capping we will use the Diamond data set. In order to cap the outliers in the carat variable, we can simply apply our user-defined function to the carat variable as follows:

Diamonds <- read.csv("data/Diamonds.csv")
carat_capped <- Diamonds$carat %>% cap()

We can also apply this function to a data frame using sapply function. Here is an example of applying cap() function to a subset of the Diamonds data frame:

# Take a subset of Diamonds data using quantitative variables

Diamonds_sub <- Diamonds %>%  dplyr::select(carat, depth, price)

# See descriptive statistics

summary(Diamonds_sub)

##      carat            depth           price      
##  Min.   :0.2000   Min.   :43.00   Min.   :  326  
##  1st Qu.:0.4000   1st Qu.:61.00   1st Qu.:  950  
##  Median :0.7000   Median :61.80   Median : 2401  
##  Mean   :0.7979   Mean   :61.75   Mean   : 3933  
##  3rd Qu.:1.0400   3rd Qu.:62.50   3rd Qu.: 5324  
##  Max.   :5.0100   Max.   :79.00   Max.   :18823

# Apply a user defined function "cap" to a data frame

Diamonds_capped <- sapply(Diamonds_sub, FUN = cap)

# Check summary statistics again

summary(Diamonds_capped)

##      carat            depth           price      
##  Min.   :0.2000   Min.   :58.80   Min.   :  326  
##  1st Qu.:0.4000   1st Qu.:61.00   1st Qu.:  950  
##  Median :0.7000   Median :61.80   Median : 2401  
##  Mean   :0.7821   Mean   :61.75   Mean   : 3812  
##  3rd Qu.:1.0400   3rd Qu.:62.50   3rd Qu.: 5324  
##  Max.   :2.0000   Max.   :64.70   Max.   :13107

Transforming and binning values

Transforming variables can also eliminate outliers. Natural logarithm of a value reduces the variation caused by outliers. Binning is also a form of variable transformation. Transforming and binning will be covered in detail in the next module (Module 7: Transform).

Outliers can also be valuable!

The outlier detection methods (i.e. Tukey’s method, z-score method) provide us ‘suggested outliers’ in the data which tend to be far away from the rest of observations. Therefore, they serve as a reminder of possible anomalies in the data.

For some applications, those anomalies would be problematic (especially for the statistical tests) and usually be handled using omitting, imputing, capping, binning or applying transformations …etc. as they can bias the statistical results.

On the other hand, for some other applications like anomaly detection or fraud detection, these anomalies could be valuable and interesting. For such cases you may choose to leave (and investigate further) those values as they can tell you an interesting story about your data.

To wrap-up: We don’t always remove, impute, cap or transform suggested outliers in the data, for some applications outliers can provide valuable information or insight therefore analysts may choose to keep those values for further investigation.