Module 7 Demonstration
Transform: Data Transformation, Standardisation, and Reduction
1 / 33

Recall: Major tasks for data preprocessing

Data Preprocessing Steps

Fig1. Major tasks in data preprocessing

Data transformation is an important step in data preprocessing for the development and deployment of statistical analysis and machine learning models.

In statistical and machine learning analyses, it is necessary to perform some data transformations on the raw (but tidy and clean!) data before it can be used for modeling.

2 / 33

Remark

Specific types of analyses may require specific types of transformations.

As you move forward in your master's program, you will learn the details of these specific transformations used in different subjects like:
- Regression Analysis
- Machine Learning
- Time Series Analysis
- Forecasting, etc.
We won't cover the technical details of these transformations.
Our focus will be on the most common and useful ones that can be easily implemented in R.

3 / 33

Why We Need to Transform Data?

Below are the situations where we might need transformations:
- To change the scale of a variable or standardise the values of a variable for better understanding.
- To transform complex non-linear relationships into a linear one (i.e. to improve linearity).
- To improve assumptions of normality and homogeneity of variance, etc (i.e., reduce skewness and/or heterogeneity of variances).

4 / 33

Activity:

Have a look at three data examples with visualizations.
Specify the reason(s) for transforming data for each case.
Press P to reveal the answers.

5 / 33

Data Set 1: Salary increase

Suppose we are looking at the salary increases of four employees:

##     name prev_salary increase
## 1   Mark      100000     5000
## 2    Sue       50000     3000
## 3 Jayden       80000     2000
## 4    Joe      120000     4000

Who got the highest increase?

6 / 33

Data Set 1: Salary increase

Suppose we are looking at the salary increases of four employees:

##     name prev_salary increase
## 1   Mark      100000     5000
## 2    Sue       50000     3000
## 3 Jayden       80000     2000
## 4    Joe      120000     4000

Who got the highest increase?

df %>% mutate(percentage_increase = (increase/prev_salary*100))

##     name prev_salary increase percentage_increase
## 1   Mark      100000     5000            5.000000
## 2    Sue       50000     3000            6.000000
## 3 Jayden       80000     2000            2.500000
## 4    Joe      120000     4000            3.333333

6 / 33

To better understand who got the highest/lowest increase we applied a simple transformation on the increase amount.
We calculated the percentage increase using percentage_increase = (increase/prev_salaryx100) to have a better undertanding.

Data set 2

Have a look at the graphs of x-y pair vs. transformed x-y pair:

7 / 33

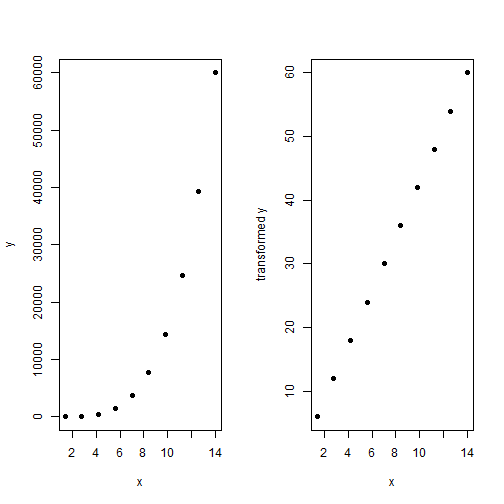
To transform complex non-linear relationships into a linear one (i.e. to improve linearity).

Data set 3

What about distribution of x values vs. transformed values:

8 / 33

To improve assumptions of normality or to reduce skewness.

Data TransformationsTransformations through mathematical operations can easily be done in R using arithmetic functions:


Transformation
Power
R function


logarithm base 10
NA
log10(y)

logarithm base e
NA
log(y)

reciprocal square
-2
y^(-2)

reciprocal
-1
y^(-1)

cube root
1/3
y^(1/3)

square root
1/2
y^(1/2) or sqrt()

square
2
y^2

cube
3
y^3

fourth power
4
y^4

9 / 33

Transformation	Power	R function
logarithm base 10	`NA`	`log10(y)`
logarithm base e	`NA`	`log(y)`
reciprocal square	-2	`y^(-2)`
reciprocal	-1	`y^(-1)`
cube root	1/3	`y^(1/3)`
square root	1/2	`y^(1/2)` or `sqrt()`
square	2	`y^2`
cube	3	`y^3`
fourth power	4	`y^4`

Recommendations on Mathematical Transformations

Here are some recommendations on mathematical transformations:
- To reduce right skewness in the distribution, taking roots or logarithms or reciprocals work well.
- To reduce left skewness, taking squares or cubes or higher powers work well.

These are general recommendations and may not work for every data set.
The best strategy is to apply different transformations on the same data and select the one that works best.

10 / 33

Log transformations are commonly used for reducing right skewness. It can not be applied to 0 or negative values directly but you can add a non-negative constant to all observations and then take the logarithm.
Square root transformation is also used for reducing right skewness, and also has the advantage that it can be applied to zero values.
Reciprocal transformation is a very strong transformation with a drastic effect on the distribution shape. It will compress large values to smaller values.

BoxCox TransformationBoxCox transformation is a type of power transformation to transform non-normal data into a normal distribution. 
This transformation is named after statisticians George Box and Sir David Cox who collaborated on a 1964 paper and developed the technique.
Normal distribution assumption is very crucial for many statistical hypothesis tests especially for the parametric hypothesis testing, linear regression, time series analysis, etc. 
11 / 33

BoxCox Transformation Cont.

Let $y$ denote the variable at the original scale and $y^{'}$ the transformed variable. The BoxCox transformation is defined as:

$y^{'} = \frac{y^{λ} - 1}{λ}, if λ \neq 0$

$y^{'} = l o g (y), if λ = 0$

As seen in the equation, the $λ$ parameter is very important for applying this transformation.

Optimum $λ$ parameter satisfying the normality assumption is found by a search algorithm or the maximum likelihood estimation.

12 / 33

BoxCox Transformation Cont.

forecast package will be used to apply BoxCox transformation and find the best $λ$ parameter.

BoxCox_x<- BoxCox(x, lambda = "auto")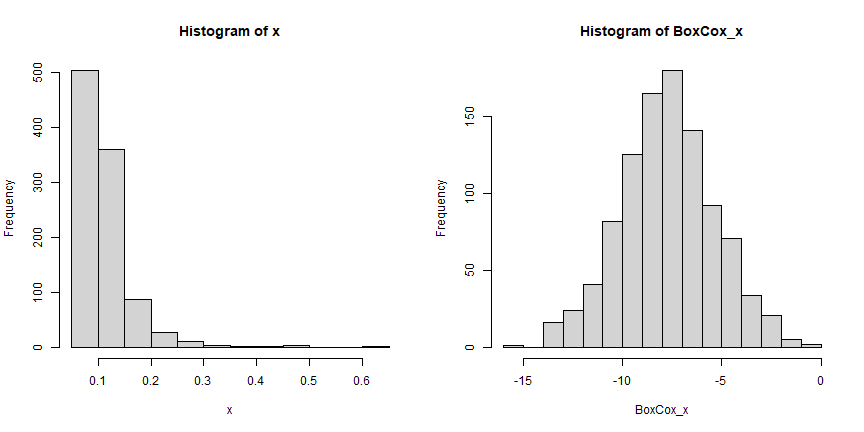

13 / 33

Activity: Your turn!

The Cars.csv data set from the data repository. This dataset contains data from over 400 vehicles from 2003.

## # A tibble: 6 × 19
##   Vehicle_name         Sports Sport_utility Wagon Minivan Pickup All_wheel_drive
##   <chr>                 <dbl>         <dbl> <dbl>   <dbl>  <dbl>           <dbl>
## 1 Chevrolet Aveo 4dr        0             0     0       0      0               0
## 2 Chevrolet Aveo LS 4…      0             0     0       0      0               0
## 3 Chevrolet Cavalier …      0             0     0       0      0               0
## 4 Chevrolet Cavalier …      0             0     0       0      0               0
## 5 Chevrolet Cavalier …      0             0     0       0      0               0
## 6 Dodge Neon SE 4dr         0             0     0       0      0               0
## # ℹ 12 more variables: Rear_wheel_drive <dbl>, Retail_price <dbl>,
## #   Dealer_cost <dbl>, Engine_size <dbl>, Cylinders <dbl>, Kilowatts <dbl>,
## #   Economy_city <dbl>, Economy_highway <dbl>, Weight <dbl>, Wheel_base <dbl>,
## #   Length <dbl>, Width <dbl>

14 / 33

Activity: Your turn!

We will focus on two variables, Economy_highway: Kilometres per liter for highway driving and Weight: weight of car (kg). Here are univariate and bivariate visualizations:

Apply transformation(s) on variable(s) to improve linearity.

15 / 33

It turns out, log() transformation is a great way to correct for skewness for this data.

par(mfrow=c(2,2))
Cars$Weight %>%  hist(main = "Weight")
log(Cars$Weight) %>%  hist(main = "log(Weight)")
Cars$Economy_highway %>%  hist(main = "Economy")
log(Cars$Economy_highway) %>%  hist(main = "log(Economy)")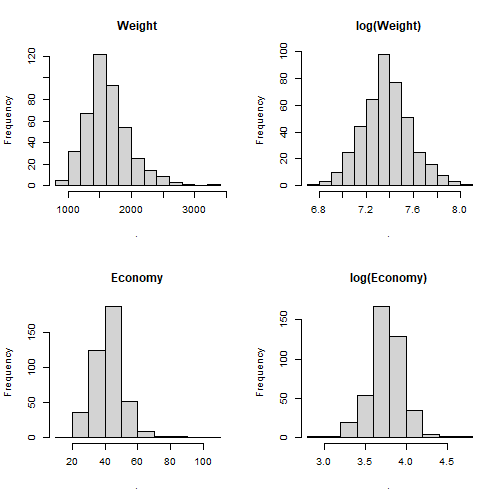

After applying the transformation, the relationship looks much more linear.

plot(log(Cars$Economy_highway), log(Cars$Weight))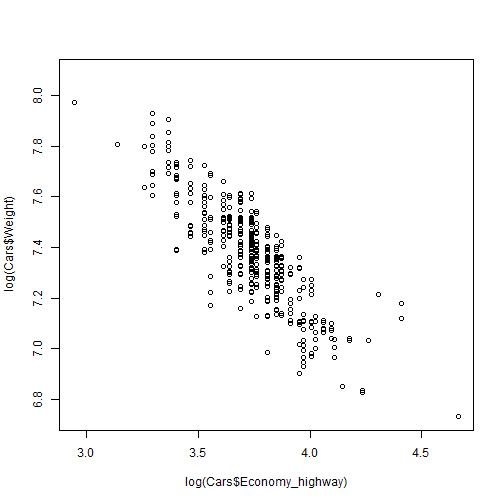

Data NormalisationSome statistical analysis methods are sensitive to the scale of the variables.
Values for one variable could range between 0-1 and values for other variable could range from 1-10000000.
As a consequence, the impact on response variables by the variables having greater numeric range (i.e., 1-10000000), could be more than the one having less numeric range (i.e. 0-1).
Especially for the distance based methods in machine learning, this could in turn impact the prediction accuracy. 
For such cases, we may need to normalize or scale the values under different variables such that they fall under common range.
16 / 33

Data Normalisation Cont.

There are different normalization techniques used in machine learning:
- Centering (using mean)
- Scaling (using standard deviation)
- z-score transformation (i.e., centering and scaling using both mean and standard deviation)
- min-max, (a.k.a. range and (0-1) ) transformation

17 / 33

Data Normalisation Cont.

Normalisation technique
Formula
R Function


Centering
y∗=y−¯yy∗=y−y¯
scale(y, center = TRUE, scale = FALSE)

Scaling (using RMS)
y∗=yRMSyy∗=yRMSy
scale(y, center = FALSE, scale = TRUE)

Scaling (using SD)
y∗=ySDyy∗=ySDy
scale(y, center = FALSE, scale = sd(y))

z-score transformation
z=y−¯ySDyz=y−y¯SDy
scale(y, center = TRUE, scale = TRUE)

Min-max transformation
y∗=y−yminymax−yminy∗=y−yminymax−ymin
(y- min(y)) /(max(y)-min(y))

18 / 33

Normalisation technique	Formula	R Function
Centering	$y * = y - \bar{y}$	`scale(y, center = TRUE, scale = FALSE)`
Scaling (using RMS)	$y * = \frac{y}{R M S_{y}}$	`scale(y, center = FALSE, scale = TRUE)`
Scaling (using SD)	$y * = \frac{y}{S D_{y}}$	`scale(y, center = FALSE, scale = sd(y))`
z-score transformation	$z = \frac{y - \bar{y}}{S D_{y}}$	`scale(y, center = TRUE, scale = TRUE)`
Min-max transformation	$y * = \frac{y - y_{m i n}}{y_{m a x} - y_{m i n}}$	`(y- min(y)) /(max(y)-min(y))`

Activity: Your turn!

Use the Cars.csv data set:

Task 1: Check the distribution of Economy_highway variable using boxplot().
Task 2: Apply z-score transformation on Economy_highway variable and check the distribution again. Did the shape of the distribution change?
Task 3: Check the distribution of `Weight variable using boxplot().

Task 4: Apply min-max transformation to Weight variable and check the distribution again. Did the shape of the distribution change?

19 / 33

# Task 1:
Cars <- read.csv("../data/Cars.csv")
boxplot(Cars$Economy_highway)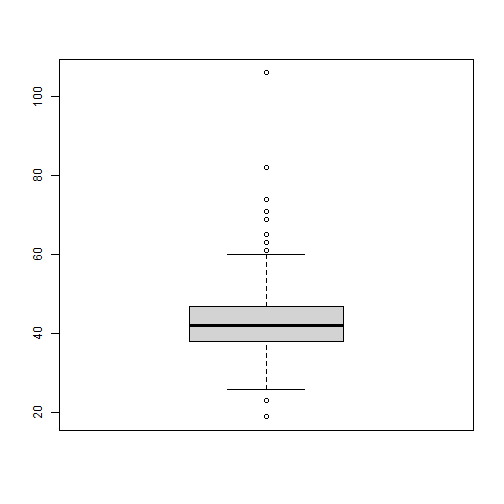

# Task 2:
z<- Cars$Economy_highway %>% scale(center = TRUE, scale = TRUE)
boxplot(z)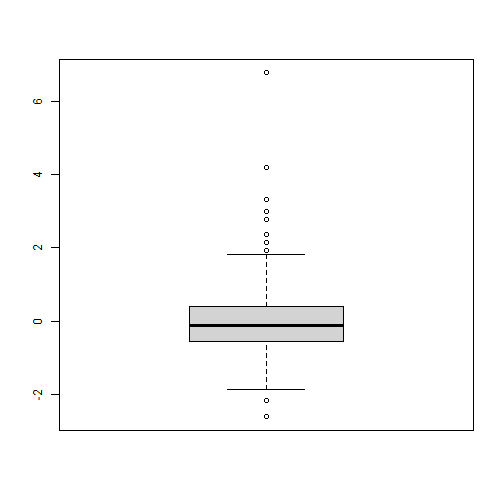

# To compare easily:
par(mfrow=c(1,2))
boxplot(Cars$Economy_highway)
boxplot(z)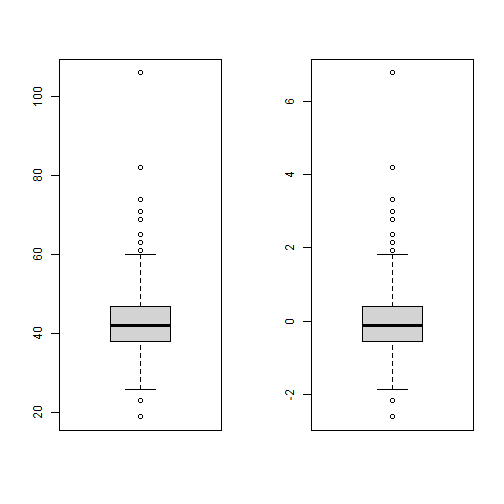

# Task 3:
boxplot(Cars$Weight)
# Task 4
minmaxnormalise <- function(x){(x- min(x, na.rm = TRUE)) /(max(x, na.rm = TRUE)-min(x,na.rm = TRUE))}
min_max <- Cars$Weight %>%  minmaxnormalise()
boxplot(min_max)
# To compare easily:
par(mfrow=c(1,2))
boxplot(Cars$Weight)
boxplot(min_max)

Remark

Main difference between transformation and normalisation:
- With transformation, the scale of the variable and its distribution will change. Thus the variable will completely be transformed.
- With normalisation, the scale of the variable will change but the distribution won't change. The variable will be mapped to a different scale but the distributional properties are kept.

20 / 33

Remark

Main difference between transformation and normalisation:
- With transformation, the scale of the variable and its distribution will change. Thus the variable will completely be transformed.
- With normalisation, the scale of the variable will change but the distribution won't change. The variable will be mapped to a different scale but the distributional properties are kept.

This is why we apply transformations to change the distributional properties of a variable (i.e., to reduce skewness, improve normality, linearity).

20 / 33

Remark

Main difference between transformation and normalisation:
- With transformation, the scale of the variable and its distribution will change. Thus the variable will completely be transformed.
- With normalisation, the scale of the variable will change but the distribution won't change. The variable will be mapped to a different scale but the distributional properties are kept.

This is why we apply transformations to change the distributional properties of a variable (i.e., to reduce skewness, improve normality, linearity).
Note that sometimes the name "transformation" is also used for "z-score transformation" and "Min-max transformation", but actually they are normalisation techniques.

20 / 33

Binning (a.k.a. Discretisation)

Sometimes we may need to discretise numeric values as analysis methods require discrete values as a input or output variables.
Binning or discretisation methods transform numerical variables into categorical counterparts by using some strategies:

Binning strategy	Function (from `infotheo`)
Equal width (distance) binning	`discretize(y, disc = "equalwidth")`
Equal depth (frequency) binning	`discretize(y, disc = "equalfreq")`

In equal-width binning, the variable is divided into $n$ intervals of equal size.
In equal-depth binning, the variable is divided into $n$ intervals, each containing approximately the same number of observations (frequencies).
As mentioned in Module 6 Scan: Outliers, binning is also useful to deal with possible outliers.

21 / 33

Data (dimension) reductionLarge data sets -> a common problem -> "curse of dimensionality" because of huge number of variables (a.k.a. features/dimensions). 
The high dimensionality will increase the computational complexity and increase the risk of overfitting (e.g. machine learning algorithms and regression techniques). 
Good news is there are ways of addressing the curse of high-dimensionality.
There are two ways of dimension reduction: feature selection and feature extraction. 
22 / 33

Data (dimension) reduction Cont.

Our focus would be on gaining brief information on each method, i.e. differences between methods, why and when they are used, etc.
We won't cover the technical details nor their implementation in R as they will be taught in the Machine Learning course in details. You may refer to the “Optional Reading” and “Additional Resources and Further Reading” sections to find out more on the topic.

23 / 33

Feature selection

In feature selection, we try to find a subset of the original set of variables, or features which are most useful or most significant.

24 / 33

Feature selection techniques

There are different strategies to select features depending on the problem that you are dealing with.
- Feature filtering
- Feature ranking

25 / 33

Feature filteringIn feature filtering, redundant features are filtered out and the ones that are most useful or most relevant for the problem are selected.
Some strategies:removing features with zero and near zero-variance;
removing/keeping highly correlated variables (i.e., greater than 0.8);
...

26 / 33

Feature rankingIn this technique features are ranked according to an importance ( a statistical) criteria and selected (or removed) from the data set if they are above a defined threshold. 
Some strategies:ranking features according to correlation test;
ranking features according to chi-square test;
ranking features according to entropy based test;
...

27 / 33

Feature extraction

Feature extraction reduces the data in a high dimensional space to a lower dimension space, i.e. linear combinations of the original features.

28 / 33

Feature selection vs. Feature extraction

Feature extraction is different from feature selection.
Both methods seek to reduce the number of attributes in the data set:
- feature extraction methods do so by creating new combinations of attributes;
- where as feature selection methods include and exclude attributes present in the data without changing them.

29 / 33

Feature extractionOne of the most commonly used approach to extract features is the principal component analysis (PCA).
PCA is an unsupervised algorithm that creates linear combinations of the original features.
30 / 33

Principal Component Analysis

The new extracted features are orthogonal, which means that they are uncorrelated.
The extracted components are ranked in order of their "explained variance". For example, the first principal component (PC1) explains the most variance in the data, PC2 explains the second-most variance, and so on.
Then you can decide to keep only as many principal components as needed to reach a cumulative explained variance of 90%.
This technique is fast and simple to implement, and works well in practice.
However the new principal components are not interpretable, because they are linear combinations of original features.

31 / 33

Functions to Remember for Week 9

Mathematical functions
BoxCox() from forecast
scale()
discretize() from infotheo
Data (dimension) reduction
Feature selection vs. Feature extraction
Feature filtering vs. ranking
Practice!

32 / 33

Class Worksheet

Working in small groups, complete the following worksheet:

Module 7 Worksheet

Once completed, feel free to work on your Assessments.

Return to Course Website

33 / 33

Recall: Major tasks for data preprocessing

Fig1. Major tasks in data preprocessing

Data transformation is an important step in data preprocessing for the development and deployment of statistical analysis and machine learning models.

In statistical and machine learning analyses, it is necessary to perform some data transformations on the raw (but tidy and clean!) data before it can be used for modeling.

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

Module 7 Demonstration

Transform: Data Transformation, Standardisation, and Reduction

Recall: Major tasks for data preprocessing

Remark

Why We Need to Transform Data?

Activity:

Data Set 1: Salary increase

Data Set 1: Salary increase

Data set 2

Data set 3

Data Transformations

Recommendations on Mathematical Transformations

BoxCox Transformation

BoxCox Transformation Cont.

BoxCox Transformation Cont.

Activity: Your turn!

Activity: Your turn!

Data Normalisation

Data Normalisation Cont.

Data Normalisation Cont.

Activity: Your turn!

Remark

Remark

Remark

Binning (a.k.a. Discretisation)

Data (dimension) reduction

Data (dimension) reduction Cont.

Feature selection

Feature selection techniques

Feature filtering

Feature ranking

Feature extraction

Feature selection vs. Feature extraction

Feature extraction

Principal Component Analysis

Functions to Remember for Week 9

Class Worksheet

Recall: Major tasks for data preprocessing

Help